Théorème de Bayes
Le théorème de Bayes, nommé d’après le mathématicien britannique du 18ème siècle, Thomas Bayes, est une formule mathématique permettant de déterminer la probabilité conditionnelle . Le théorème fournit un moyen de réviser les prédictions ou théories existantes (probabilités de mise à jour) à partir de preuves nouvelles ou supplémentaires. En finance, le théorème de Bayes peut être utilisé pour évaluer le risque de prêt d’argent à des emprunteurs potentiels.
Le théorème de Bayes est également appelé règle de Bayes ou loi de Bayes et constitue le fondement du domaine de la statistique bayésienne.
Retenons
- Le théorème de Bayes vous permet de mettre à jour les probabilités prédites d’un événement en incorporant de nouvelles informations.
- Le théorème de Bayes a été nommé d’après le mathématicien Thomas Bayes du 18ème siècle.
- Il est souvent employé en finance pour mettre à jour l’évaluation des risques.
La formule pour le théorème de Bayes est
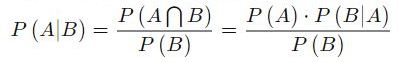
P( A )= La probabilité que A se produise
P( B )= La probabilité que B se produise
P( A ∣ B )= probabilité conditionnelle de A sachant B.
P( B ∣ A )= probabilité conditionnelle de B sachant A.
P( A⋂B ) )= La probabilité que A et B se produisent.
Le théorème de Bayes expliqué
Les applications du théorème sont répandues et ne se limitent pas au domaine financier. À titre d’exemple, le théorème de Bayes peut être utilisé pour déterminer l’exactitude des résultats d’un test médical en prenant en compte la probabilité qu’une personne donnée soit atteinte d’une maladie et l’exactitude générale du test. Le théorème de Bayes repose sur l’incorporation de distributions de probabilité antérieures afin de générer des probabilités postérieures. La probabilité préalable, dans l’inférence statistique bayésienne, est la probabilité d’un événement avant la collecte de nouvelles données. C’est la meilleure évaluation rationnelle de la probabilité d’un résultat basée sur les connaissances actuelles avant la réalisation d’une expérience. La probabilité postérieure est la probabilité révisée qu’un événement se produise après la prise en compte de nouvelles informations. La probabilité a posteriori est calculée en mettant à jour la probabilité précédente en utilisant le théorème de Bayes. En termes statistiques, la probabilité postérieure est la probabilité que l’événement A se produise étant donné que l’événement B s’est produit.
Le théorème de Bayes donne donc la probabilité d’un événement sur la base de nouvelles informations qui sont ou peuvent être liées à cet événement. La formule peut également être utilisée pour voir comment la probabilité qu’un événement se produise est affectée par de nouvelles informations hypothétiques, en supposant que les nouvelles informations se révèlent vraies. Par exemple, supposons qu’une seule carte soit tirée d’un jeu complet de 52 cartes. La probabilité que la carte soit un roi est 4 divisée par 52, ce qui équivaut à 1/13 ou environ 7,69%. Rappelez-vous qu’il y a 4 rois dans le pont. Supposons maintenant que la carte sélectionnée est une carte de visage. La probabilité que la carte sélectionnée soit un roi, étant donné que c’est une carte visage, est 4 divisé par 12, ou environ 33,3%, car il y a 12 cartes faciales dans un jeu de 54 cartes.
Exemple numérique du théorème de Bayes
A titre d’exemple, imaginons qu’un détecteur de mensonge présente une exactitude de 98%, c’est-à-dire que 98% du temps, il montre un résultat véritablement positif pour les menteurs et 98% du temps, un résultat véritablement négatif pour les véridiques. Ensuite, supposons que 0,5% des personnes mentent. Si une personne sélectionnée au hasard présente un résultat positif pour ses dires, le calcul suivant peut être effectué pour déterminer si la probabilité présente réellement un menteur.
(0,98 x 0,005) / [(0,98 x 0,005) + ((1 – 0,98) x (1 – 0,005))]] = 0,0049 / (0,0049 + 0,0199) = 19,76%
Le théorème de Bayes montre que même si une personne est détectée comme étant menteuse dans ce scénario, il est en réalité beaucoup plus probable qu’elle ne soit pas une menteuse.