Théorème central limite
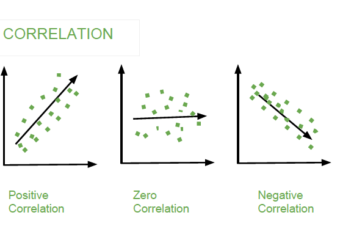
Dans l’étude de la théorie des probabilités, le théorème central limite (TCL) stipule que la distribution des moyennes d’échantillon se rapproche d’une distribution normale (également appelée «courbe en cloche»), à mesure que la taille de l’échantillon augmente, en supposant que tous les échantillons sont identiques quelle que soit la forme de la répartition de la population.
En d’autres termes, le TCL est une théorie statistique stipulant que, compte tenu de la taille suffisante d’un échantillon d’une population présentant un niveau de variance fini, la moyenne de tous les échantillons de la même population sera approximativement égale à la moyenne de la population. En outre, tous les échantillons suivront un schéma de distribution approximativement normal , toutes les variances étant approximativement égales à la variance de la population, divisées par la taille de chaque échantillon.
Bien que ce concept ait été développé pour la première fois par Abraham de Moivre en 1733, il n’a été officiellement désigné qu’en 1930. Le mathématicien hongrois George Polya l’a surnommé officiellement le théorème central limite (Central Limit Theorem (CLT)).
Comprendre le théorème central limite
Selon le théorème central limite, la moyenne d’un échantillon de données sera plus proche de la moyenne de l’ensemble de la population en question, à mesure que la taille de l’échantillon augmentera, indépendamment de la distribution réelle des données. En d’autres termes, les données sont précises, que la distribution soit normale ou aberrante.
En règle générale, des tailles d’échantillon égales ou supérieures à 30 sont considérées comme suffisantes pour que le TCL se maintienne, ce qui signifie que la distribution de la moyenne de l’échantillon est assez normalement. Par conséquent, plus on prélève d’échantillons, plus les résultats graphiques prennent la forme d’une distribution normale.
Le théorème central limite présente un phénomène où la moyenne de la moyenne de l’échantillon et des écarts-types sont égaux à la moyenne de la population et à l’écart-type, ce qui est extrêmement utile pour prédire avec précision les caractéristiques des populations.
Retenons
- Le théorème central limite (TCL) stipule que la distribution des moyennes d’échantillon se rapproche d’une distribution normale lorsque la taille de l’échantillon augmente.
- Des tailles d’échantillon égales ou supérieures à 30 sont considérées comme suffisantes pour que le TCL puisse tenir.
- Un aspect clé du TCL est que la moyenne des moyennes d’échantillon et des écarts-types seront égaux à la moyenne de la population et à l’écart-type.
- Une taille d’échantillon suffisamment grande peut permettre de prédire avec précision les caractéristiques d’une population.
Le théorème central limite en finance
Le TCL est utile lorsque vous examinez les rendements d’une action individuelle ou d’indices plus larges, car l’analyse est simple, en raison de la facilité relative à générer les données financières nécessaires. Par conséquent, les investisseurs de tous types comptent sur le TCL pour analyser les rendements des actions, constituer des portefeuilles et gérer les risques.
Par exemple, un investisseur souhaite analyser le rendement global d’un indice boursier composé de 1 000 actions. Dans ce scénario, cet investisseur peut simplement étudier un échantillon aléatoire d’actions, afin de cultiver les rendements estimés de l’indice total. Pour que le théorème central limite soit respecté, il faut échantillonner au moins 30 actions sélectionnées de manière aléatoire dans différents secteurs. En outre, les actions précédemment sélectionnées doivent être échangées avec des noms différents pour aider à éliminer les biais.