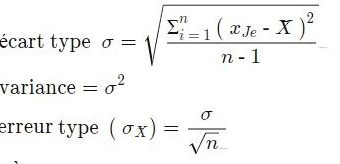Modèle d’évaluation des actifs financiers (MEDAF): avantages et inconvénients
Le modèle d’évaluation des actifs financiers (MEDAF), une fois mis en pratique, présente des avantages et des inconvénients.
Modèle MEDAF: un aperçu
Le modèle d’évaluation des actifs financiers (MEDAF) est une théorie financière qui établit une relation linéaire entre le retour sur investissement requis et le risque. Le modèle est basé sur la relation entre le bêta d’ un actif , le taux sans risque (généralement le taux des bons du Trésor ) et la prime de risque sur actions, ou le rendement attendu sur le marché moins le taux sans risque.
Ra = Rrf + βa * (Rm– Rrf)
où
Ra =Rentabilité espérée de l’actif financier
Rrf =Taux sans risque
Rm=Rentabilité espérée du marché
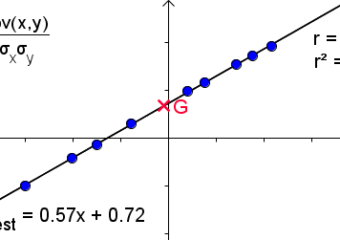
βa = La volatilité de la rentabilité de l’actif considéré rapportée à celle du marché. Mathématiquement parlant, elle correspond au rapport entre la covariance de la rentabilité de l’actif et de la rentabilité du marché et la variance de la rentabilité du marché.
Rm– Rrf = prime de risque du marché.
Au cœur du modèle se trouvent ses hypothèses sous-jacentes, que beaucoup jugent irréalistes et qui pourraient constituer la base de certains de ses principaux inconvénients. Aucun modèle n’est parfait, mais chacun devrait avoir quelques caractéristiques qui le rendent utile et applicable.
Avantages du modèle MEDAF
L’application du MEDAF présente de nombreux avantages, notamment:
Facilité d’utilisation
Le MEDAF est un calcul simple qui peut être facilement soumis à des tests de résistance pour dériver une gamme de résultats possibles afin de fournir une confiance autour des taux de rendement requis.
Retenons
- Le MEDAF est un modèle de retour largement utilisé qui est facilement calculé et testé sous contrainte.
- Il est critiqué pour ses hypothèses irréalistes.
- Malgré ces critiques, le modèle MEDAF fournit un résultat plus utile que le Modèle de Gordon et Shapiro ou le modèle CMPC dans de nombreuses situations.
Portefeuille diversifié
L’hypothèse selon laquelle les investisseurs détiennent un portefeuille diversifié, similaire au portefeuille de marché, élimine le risque non systématique (spécifique) .
Risque systématique
Le MEDAF prend en compte le risque systématique (bêta), qui est exclu des autres modèles de rendement, tels que le modèle d’actualisation des dividendes (DDM). Le risque systématique ou de marché est une variable importante car il est imprévu et, pour cette raison, ne peut souvent pas être complètement atténué.
Variabilité des risques commerciaux et financiers
Lorsque les entreprises recherchent des opportunités, si la composition de l’entreprise et le financement diffèrent de l’entreprise actuelle, d’autres calculs de rendement requis, comme le coût moyen pondéré du capital (CMPC), ne peuvent pas être utilisés. Ce qui n’est pas le cas de MEDAF.
Lorsqu’il est utilisé conjointement avec d’autres aspects d’une mosaïque d’investissement, le MEDAF peut fournir des données de rendement inégalées qui peuvent soutenir ou éliminer un investissement potentiel.
Inconvénients du modèle MEDAF
Comme de nombreux modèles scientifiques, le MEDAF a ses inconvénients. Les principaux inconvénients se reflètent dans les données d’entrée et les hypothèses du modèle, notamment:
Taux sans risque (Rf)
Le taux communément utilisé comme R f est le rendement des titres d’État à court terme . Le problème avec l’utilisation de cette entrée est que le rendement change quotidiennement, créant de la volatilité .
Rentabilité espérée du marché (Rm)
Le rendement du marché peut être décrit comme la somme des gains en capital et des dividendes du marché. Un problème survient lorsque, à un moment donné, le rendement du marché peut être négatif. Par conséquent, un rendement du marché à long terme est utilisé pour lisser le rendement. Un autre problème est que ces rendements sont rétrospectifs et peuvent ne pas être représentatifs des rendements futurs du marché.
Capacité d’emprunter à un taux sans risque
Le MEDAF repose sur quatre hypothèses principales, dont une qui reflète une image irréaliste du monde réel. Cette hypothèse – que les investisseurs peuvent emprunter et prêter à un taux sans risque – est inatteignable en réalité. Les investisseurs individuels ne sont pas en mesure d’emprunter (ou de prêter) au même taux que le gouvernement. Par conséquent, la ligne de retour minimale requise peut en fait être moins raide (fournir un retour inférieur) que le modèle ne le calcule.