Droite de marché des capitaux
Qu’est-ce que la droite du marché des capitaux?
La droite du marché des capitaux représente des portefeuilles qui combinent de manière optimale risque et rendement. Le modèle d’évaluation des immobilisations décrit le compromis entre le risque et le rendement pour des portefeuilles efficaces. C’est un concept théorique qui représente tous les portefeuilles combinant de manière optimale le taux de rendement sans risque et le portefeuille de marché des actifs risqués. Sous le modèle d’évaluation des immobilisations, tous les investisseurs choisiront une position sur la ligne du marché des capitaux, en équilibre, en empruntant ou en prêtant au taux sans risque, car cela maximise le rendement pour un niveau de risque donné.
Retenons
- La droite du marché des capitaux représente des portefeuilles qui combinent de manière optimale risque et rendement.
- La droite du marché des capitaux est un cas particulier de la droite d’allocation du capital où le portefeuille de risque est le portefeuille de marché. Ainsi, la pente de la droite du marché des capitaux est le ratio de sharpe du portefeuille de marché.
- Le point d’interception de la droite du marché des capitaux et de l’efficacité de la frontière donneraient lieu au portefeuille le plus efficace appelé portefeuille de tangence.
- En règle générale, achetez des actifs si le ratio de partage est supérieur à la droite du marché des capitaux et vendez-le si le ratio de sharpe est inférieur à la droite du marché des capitaux.
Comprendre la droite du marché des capitaux
Les portefeuilles qui tombent sur la droite du marché financier optimisent en théorie la relation risque / rendement, maximisant ainsi la performance. La droite d’allocation de capital constitue l’allocation des actifs sans risque et du portefeuille risqué pour un investisseur. La droite du marché des capitaux est un cas particulier de la droite d’allocation du capital où le portefeuille de risque est le portefeuille de marché. Ainsi, la pente de la droite du marché des capitaux est le ratio de sharpe du portefeuille de marché. En règle générale, achetez des actifs si le ratio de sharpe est supérieur à la droite du marché des capitaux et vendez-les si le ratio de sharpe est inférieur à la droite du marché des capitaux .
La droite du marché des capitaux se distingue de la frontière efficiente plus populaire en ce qu’elle inclut des investissements sans risque. Le point d’interception de la droite du marché des capitaux et de l’efficacité de la frontière donneraient le portefeuille le plus efficace, appelé portefeuille de tangence.
Le modèle d’évaluation des actifs financiers (MEDAF) est la ligne qui relie le taux de rendement sans risque au point de tangence à la frontière efficiente des portefeuilles optimaux offrant le rendement attendu le plus élevé pour un niveau de risque défini ou le risque le plus faible pour un niveau de rendement attendu donné. .Les portefeuilles offrant le meilleur compromis entre rendements attendus et variance (risque) se situent sur cette droite. Le point de tangence est le portefeuille optimal d’actifs risqués, appelé portefeuille de marché. Selon les hypothèses de l’ analyse de la variance moyenne , à savoir que les investisseurs cherchent à maximiser le rendement attendu pour un montant donné de risque de variance et qu’il existe un taux de rendement sans risque, tous les investisseurs sélectionneront des portefeuilles appartenant à la droite du marché des capitaux .
Selon le théorème de séparation de Tobin, trouver le portefeuille de marché et la meilleure combinaison de ce portefeuille de marché et de l’actif sans risque est un problème distinct. Les investisseurs individuels détiendront soit uniquement l’actif sans risque, soit une combinaison de l’actif sans risque et du portefeuille de marché, en fonction de leur aversion pour le risque. Lorsqu’un investisseur monte dans la droite du marché des capitaux, le risque et le rendement globaux du portefeuille augmentent. Les investisseurs peu enclins à prendre des risques choisiront des portefeuilles proches de l’actif sans risque, préférant une faible variance à des rendements plus élevés. Les investisseurs moins enclins à prendre des risques préféreront des portefeuilles plus haut que la droite du marché des capitaux, avec un rendement attendu plus élevé, mais plus de variance. En empruntant des fonds au taux sans risque, ils peuvent également investir plus de 100% de leurs fonds pouvant être investis dans le portefeuille du marché à risque.
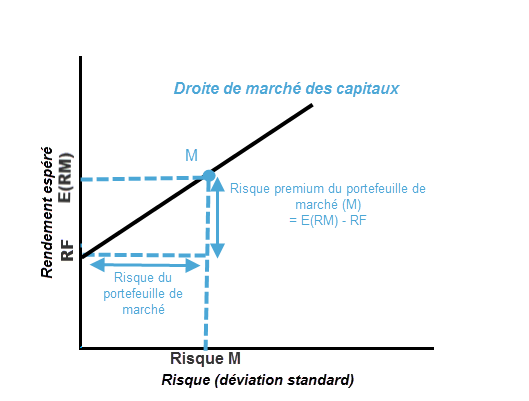
- RF correspond au taux sans risque
- E(RM) correspond au rendement espéré du portefeuille de marché
- Risque M correspond à la déviation standard du portefeuille de marché
L’équation de la droite du marché des capitaux
Rp = RF + ((E(RM) – RF) / Risque M)) x Risque p
- Rp: rendement du portefeuille
- RF: taux sans risque
- E(RM): rendement du marché
- Risque M: écart type des rendements du portefeuille
- Risque p: écart type des rendements du marché
La droite de marché des capitaux et la droite de marché des titres
La droite du marché des capitaux est parfois confondue avec la droite de marché des titres. La droite de marché des titres est dérivée de la droite du marché des capitaux. Alors que la droite du marché des capitaux affiche les taux de rendement d’un portefeuille spécifique, la droite de marché des titres représente le risque et le rendement du marché à un moment donné, ainsi que les rendements attendus des actifs individuels. Et si la mesure du risque dans la droite du marché des capitaux est l’écart type des rendements (risque total), la mesure du risque dans la droite de marché des titres est le risque systématique, ou bêta. Les titres dont le prix de revient est raisonnable figureront sur la droite du marché des capitaux et la droite de marché des titres. Les titres dont la valeur dépasse la droite du marché des capitaux ou la droite de marché des titres génèrent des rendements trop élevés pour le risque donné et sont sous-évalués. Les titres dont le tracé est inférieur à droite du marché des capitaux ou à la droite de marché des titres génèrent des rendements trop faibles pour le risque donné et sont surévalués.
Histoire de la droite du marché des capitaux
Harry Markowitz et James Tobin ont été les premiers à analyser la variance moyenne. Markowitz a identifié la frontière efficiente des portefeuilles optimaux en 1952 et James Tobin a intégré la théorie du taux sans risque à la théorie des portefeuilles modernes en 1958. William Sharpe développa ensuite le MEDAF dans les années 1960 et remporta un prix Nobel pour son travail en 1990, avec Markowitz et Merton Miller.