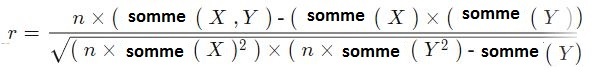Corrélation, finance

La corrélation, dans les secteurs de la finance et de l’investissement, est une statistique qui mesure le degré de mouvement de deux titres l’un par rapport à l’autre. Les corrélations sont utilisées dans la gestion de portefeuille avancée , calculée comme le coefficient de corrélation , dont la valeur doit être comprise entre -1,0 et +1,0.

La formule de corrélation est :

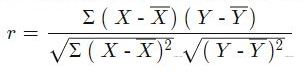
Où:
r=le coefficient de corrélation
X̄=la moyenne des observations de la variable X
Ȳ =la moyenne des observations de la variable Y

Explication de la corrélation

Une corrélation positive parfaite signifie que le coefficient de corrélation est exactement égal à 1. Cela implique que lorsqu’une sécurité se déplace, que ce soit à la hausse ou à la baisse, l’autre sécurité se déplace parallèlement, dans le même sens. Une corrélation négative parfaite signifie que deux actifs se déplacent dans des directions opposées, tandis qu’une corrélation nulle n’implique aucune relation.

Par exemple, les fonds communs de placement à grande capitalisation ont généralement une forte corrélation positive très proche de 1. Les actions de petite capitalisation ont une corrélation positive avec ce même indice, mais il n’est pas aussi élevé – généralement autour de 0,8.

Cependant, les prix des options de vente et les cours de leurs actions sous-jacentes auront tendance à avoir une corrélation négative. Lorsque le cours de l’action augmente, les prix des options de vente baissent. Il s’agit d’une corrélation négative directe et de grande magnitude.

Retenons

• La corrélation est une statistique qui mesure le degré de relation entre deux variables.
  En finance, la corrélation permet de mesurer le mouvement d’une action par rapport à celui d’un indice de référence, tel que la bêta.
• La corrélation mesure l’association, mais ne vous dit pas si x cause y ou inversement, ou si l’association est causée par un troisième facteur (peut-être invisible).

Exemple de corrélation

Les gestionnaires de portefeuille, les traders et les analystes estiment qu’il est très important de calculer la corrélation, car les avantages de la diversification en termes de réduction du risque reposent sur cette statistique. Les tableurs financiers et les logiciels peuvent calculer rapidement la valeur de la corrélation.

A titre d’exemple hypothétique, supposons qu’un analyste ait besoin de calculer la corrélation pour les deux ensembles de données suivants:

X: (41, 19, 23, 40, 55, 57, 33)

Y: (94, 60, 74, 71, 82, 76, 61)

Il faut trois étapes pour trouver la corrélation. La première consiste à additionner toutes les valeurs X pour trouver somme (X), à additionner toutes les valeurs Y pour financer somme (Y), à multiplier chaque valeur X par la valeur Y correspondante et à les additionner pour trouver Somme (X, Y). :

SOMME (X) = (41 + 19 + 23 + 40 + 55 + 57 + 33) = 268

SOMME (Y) = (94 + 60 + 74 + 71 + 82 + 76 + 61) = 518

SOMME (X, Y) = (41 x 94) + (19 x 60) + (23 x 74) + … (33 x 61) = 20 391

L’étape suivante consiste à prendre chaque valeur X, à la corriger et à résumer toutes ces valeurs pour trouver somme (x ²). La même chose doit être faite pour les valeurs Y:

SOMME (X²) = (41²) + (19²) + (23²) + … (33²) = 11 534

SOMME (Y²) = (94²) + (60²) + (74²) + … (61²) = 39 174

En notant qu’il y a sept observations, n, la formule suivante peut être utilisée pour trouver le coefficient de corrélation, r:

Articles similaires:

Fonds de roulement Corrélation négative Rentabilité des actifs nets (RONA) Échantillonnage aléatoire stratifié Théorème de Bayes Évaluation d’une entreprise selon la méthode du revenu résiduel

Tags: Analyse financière